
음악의 의의
음악이란 '음(音)'에 의한 예술입니다. 이 무한한 가능성을 가진 여러 음들 속에서 그때그때의 사회나 또는 민족에 따라 필요한 음이 선택되고 배합되어 음조직이 만들어지고 이러한 음들을 소재로 하여 음악이 만들어지는 것입니다.
페티스(Francais Joseph Fetis, 1784~1871) 19C -벨기에의 음악학자는 '음악이란 음의 배합에 의하여 사람의 감정을 감동시키는 예술'이라고 정의하고 있습니다. 즉, 음악이란 무의미한 음의 나열이 아닌, 어떠한 느낌을 이르키게 함으로써 예술로서의 음악으로 태어나게 됩니다. 그러므로 거기에는 인간의 사상이나 감정이 표현되어 있어야 하며, 그것이 한정된 시간 안에서 소리로 나타나야만 되는 것입니다. 회화나 조각이 공간적 예술임에 반하여, 음악을 시간적 예술이라고 하는 이유도 바로 여기에 있습니다. 언뜻 생각하기에 물체의 진동이나 공중의 전파도 음악이라고 할 수 있을 것 같으나, 음악 감상의 대상은 반드시 시간적으로 배열되는 음의 변화이어야 하기 때문에 이들이 음의 예술이 될 수는 없습니다. 예를 들어 회화와 비교한다면, 시간은 '화면'에 해당될 것이고 음은 '점(點점찍을 점)'에 비교될 수 있습니다. 점이 움직여서 선이 되듯이 음이 움직여서 멜로디가 됩니다. 또한 미술에서의 색채는 음 빛깔에 해당되며, 색채의 농도는 셈여림에 비할 수 있습니다.
소리에 대한 이해
소리는 물체의 진동이 공기의 파장을 통하여 사람의 고막에 전달되는 것으로 본직적으로 음색(timre), 음고(pitch)와 셈여림(intensity)으로 파악할 수 있습니다.
음색이란?
음색은 배음(overtone)으로써 결정된다. 우리는 음색으로 같은 크기와 높이의 두 개의 소리를 구분할 수 있습니다. 모든 소리는 주파수(frequency) 혹은 음파(sound wave)로 이루어져 있으며, 특히 음악에 쓰이는 많은 소리는 기본 주파수(fudamental tone)와 그것의 배음들로 이루어져 있습니다. 우리가 흔히 연주하는 악보에 기보 되어 있는 음들은 기본 주파수를 뜻 하지만 만약 악기가 배음이 없이 기본 주파수만을 낸다면 모든 악기는 정현파(sine wave)만을 발생하게 되어 결국 똑같은 음색을 낼 것이다. 음악에서 쓰이는 피아노, 관악기, 현악기 등의 소리는 대부분 제 6배음 이상의 소리를 포함하는 소리이며, 기본 주파수와 배음들이 동시에 울려서 만들어지는 복합파(complex wave)입니다.
( 기본 주파수+배음=복합파)
복합파의 구조




음과 진동
음은 진동 상태에 따라 순음(Pure tone), 고른음(Musical Tone), 시끄러운음(Noise)의 세 가지로 구분된다.
1. 순음
순음은 배음을 포함하지 않는 가장 기본적이고 단순한 진동 소리이며 단순음 도는 단음이라고 한다. 라디오에서 시보를 알리는 소리나 음차를 부드러운 해머로 조용히 두드릴 때 나는 소리가 바로 이것이다. 보통 악기에서는 이러한 소리, 즉 순음은 나지 않습니다.
2. 고른음
탄력 있는 물체의 규칙적이고 주기적인 진동으로 생긴 음입니다. 즉, 1초간의 진동수가 440이라면, 이것이 매초 주기적으로 반복되는 소리를 말합니다. 이에 따라서 일정한 음의 높이를 알 수 있고 보통 몇 개의 배음을 포함하고 있습니다. 정리하면 물체의 진동에 의해 생긴 파형이 일정하고 주기적인 음을 말합니다. 타악기를 제외한 대부분의 악기와 사람의 목소리가 여기에 속하며 음악에 주로 쓰이는 것입니다.
3. 시끄러움은
진동의 상태가 매우 불규칙하고 복잡하여 그 성질을 뚜렷이 알 수 없습니다. 시끄런음의 예시로는 물체가 부딪치는 소리나 타악기 소리, 기침소리, 소음 등을 들 수 있는데 명확한 진동수가 측정되지 않으므로 음의 높이를 알 수 없습니다.
음악에 쓰이는 음은 대게가 고른음이지만, 타악기 등 시끄러운 음도 쓰입니다. 이러한 소음의 사용은 현대에 올수록 다양해졌으며, 구체 음악이나 전자음악 등과 같은 전위음악에서는 시끄런 음만으로 구성되거나 순음까지도 사용되는 음악이 있습니다.
4. 음의 진동
음은 어떠한 원인으로 공기가 진동함으로써 발생합니다. 이 원인으로는 물체의 진동이 가장 많고, 성대 및 전기에 의한진동(스피커), 또는 고나 악기와 같은 공기 자체의 밀도의 정도 차에 의한 것도 있습니다. 이러한 공기의 진동은 음파(sound wave)가 되어 공기를 통해 귀를 자극함으로써 음의 감각을 느끼게 되는 것입니다.
하나의 현의 음 진동 원리
하나의 현 AB가 튕겨졌을 때 AB는 상하 XY로 운동하게 된다. 이 운동이 1 진동(A vibration)이며, 1초 동안 되풀이되는 횟수를 진동수 또는 주파수(Frequency)라고 합니다. 또한 XY를 진폭(Amplitude)이라고 합니다.
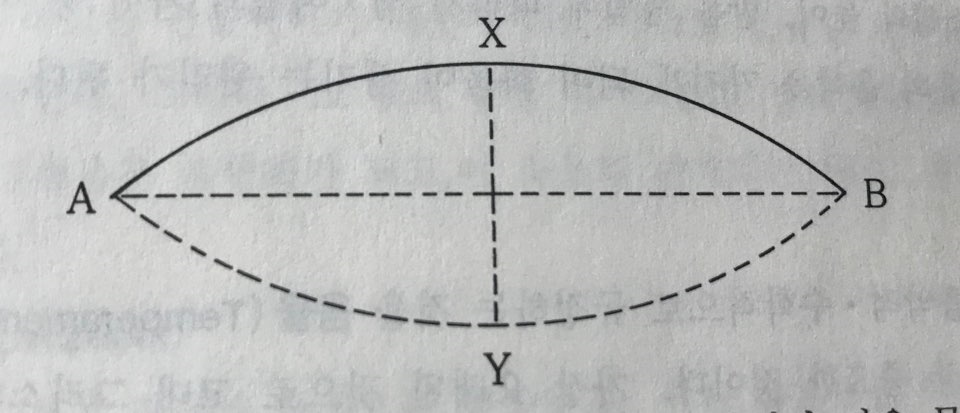
그러나 현의 진동은 이와 같은 단진동 만이 아니고 아래와 같이 무수한 진동이 동시에 일어나고 있는 것입니다.

이러한 부분은 AB가 1 진동하는 사이에 AC는 2 진동, AD는 3 진동… 이렇게 나아가게 됩니다. 이경우 단진동으로 발생하는 음을 기초음(Fundamental tone)이라 부르고, 그 밖의 부분 진동으로 발생하는 음을 상음(Partials or Overtones)이라고 합니다.
결국 한 현의 진동에 의해서 발생하는 음은 이러한 기초음과 많은 상음을 포함한 복합음인 것입니다.
배음
악기에서 하나의 음을 소리 낼 때 인간의 귀에 단순히 한 개의 음으로 들리지만 대부분의 고름음은 복합파 이므로 실제로는 여러 개의 배음이 겹쳐서 울리고 있습니다.
각 상음의 진동수가 기초음의 진동수의 정수배가 되는 것을 배음(Harmonic overtones or Harmoics)이라고 합니다.
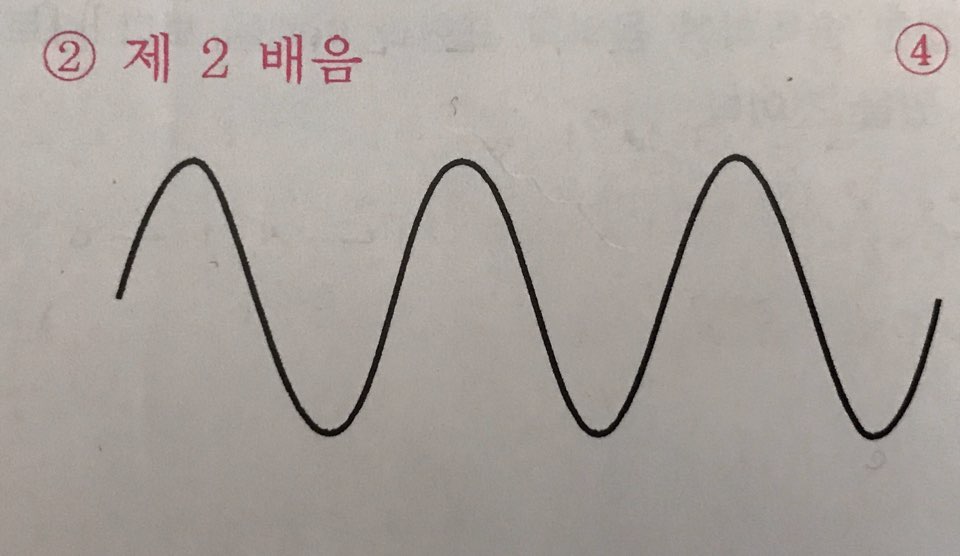
예를 들면 100Hz의 음을 목적으로 내면 그것의 정배수가 되는 200Hz 300Hz 400Hz의 배음들이 발생하게 됩니다. 그 원리의 예로 현의 길이를 1/2,1/3,1/4...로 분할함에 따라 그 진동수도 2배, 3배, 4배... 의 음이 되는데, 그 배수에 따라 제 2배음, 제 3배음, 제 4배음... 등으로 불립니다. 이렇게 진동에 의해 생겨나는 배음 들은 수 없이 많으나 우리가 일반적으로 구분할 수 있는 16번째 배음까지를 배음의 범위에 포함시키는 것이 보통입니다.

*제7음부터 16음까지는 미분음이므로 근사치를 구한 것입니다.
*목적은음 신음이 되고 제2배 음부터 제 16배음까지의 모든 배음은 여린음이 됩니다.
이러한 배음은 악기의 소리높이, 발음 방법에 다라서 셈여림의 차이 등 여러 가지 경우가 생기는데, 이러한 복합음의 어울림으로 각 악기들이 고유한 음 빛깔을 지니게 되며, 이 원리로 화음이 생기게 됩니다.
진동과 음의 관계
음은 물체의 진동으로 생겨나며, 음악에 사용되는 음은 악기를 통하여 의도하는 높이와 길이의 음을 얻게 됩니다. 이때 ,악기의 진동 시간을 길게 하면 긴음, 짧게 하면 짧은 음이 되며 악기의 발성체를 세게 진동하게 되면 센음, 여리게 진동하면 여린음이 됩니다. 또한 동일한 시간에 진동의 수를 많게 하면 높은음, 적게 하면 낮은음을 낼 수 있습니다.
*음의 성질
-높낮이: 일정한 시간 내의 진동수에 의해 결정됩니다. ex) 진동수가 많을수록 고음이 납니다.
-셈여림: 진동 에너지의 크기에 따라라 결정됩니다. ex) 진동폭이 넓을수록 센음이납니다.
-리듬: 진동 시간의 길에 따라 결정됩니다. ex) 진동 지속시간과 일치
-음색: 같은 높이의 음이라도 악기 종류, 소리 내는 방법에 따라 달라집니다.
참고문헌 大学音乐理论 白秉東著, 교학사
'MUSIC STORY' 카테고리의 다른 글
| [Theory of Music] 음악의 정의- 음악의 형태 (0) | 2020.06.09 |
|---|---|
| [Theory of Music]음악의 정의- 음악의 요소 (0) | 2020.06.08 |
| [Theory of Music] 음악의 정의-순정율과 평균율 (0) | 2020.06.05 |


