
음악의 정의 두 번째 시간입니다.
오늘은 순정율과 평균율에 대해 포스팅하겠습니다.
먼저 순정률과 평균율은 도대체 뭘까요?
음높이의 상화 관계를 음악적 그리고 수학적으로 규정하는 것을음률(Temperament)이라 하는데, 이는 음악이론의 기초를 이루는 가장 중요한 요소입니다. 가장 오래된 것으로 고대 그리스의 5도 음정을 쌓아 올린 음률이 있고, 유명한 피타고라스(Pythagoras) 음계는 이를 바탕으로 한 것입니다. 그 후, 중세의 순정률을 거쳐 18세기의 평균율에 이른 것처럼 음악 양식의 변화에 따라 점차 개량되었습니다.
순정율(Pure temperament)
-순정률은 순정 음정에 의해 음계를 구성하는 방법입니다. 사람의 귀는 두 음의 진동 비가 단순할수록 어울게 느끼고, 복잡할수록 어울리지 않게 느끼는 성질을 가지고 있습니다.
| 어울림음정의 진동비 | |||
| 음정 | 진동비 | 음정 | 진동비 |
| 완전 1도 | 1 : 1 | 장 3도 | 4 : 5 |
| 완전 8도 | 1 : 2 | 단 3도 | 5 : 6 |
| 완전 5도 | 2 : 3 | 장 6도 | 3 : 5 |
| 완전 4도 | 3 : 4 | 단 6도 | 5 : 8 |
두 음의 진동비가 정확하게 2:3 일 때, 이 두음은 순정적인 완전 5도 음정이라고 합니다. 그리고 완전 8도인 1:2의 비율이 33:65일 때는 순정적인 완전 8도가 아닌 불협화적인 완전 8도가 되는 것입니다.
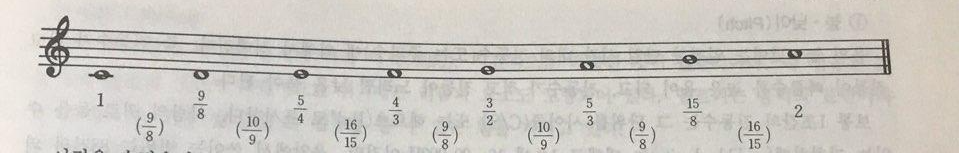
위의 사진은 순정률에 의한 장음계입니다.(괄호 안의 숫자는 인접하는 음끼리의 진동 비) 여기서 알 수 있는 것은 , C와 D, D와 E사이의 장 2도는 그 비가 9/8,10/9으로 다르다는 점입니다. 그리고 D와 A사이의 5도를 계산해 보면 진동 비는 40/27이 되고, 완전 5도의 3/2와는 차이가 있습니다. 그러므로 울림은 매우 아름답지만 전조가 불가능합니다.
| 주요 3화음을 구성하는 각 음의 진동비 | |
| 으뜸화음 (C,E,G) | 1: 5/4 : 3/2 → 4 : 5 : 6 |
| 버금딸림화음 (F,A,C) | 4/3 : 5/3 : 2 → 4 :5 : 6 |
| 딸림화음 (G,B,D) | 3/2 : 15/8 : 9/8 × 2→ 4 :5 : 6 |
이와 같이 세 화음이 똑같은 진동 비이기 때문에 C Major(다장조)로 조율된 악기로 C Major(다장조)의 악곡을 연주하면 매우 아름답게 들립니다. 그러나 그 밖의 음정, 즉 D음 상의 완전 5도는 진동 비가 27:40이므로 D음의 장 3, 단 3화음은 불협화음이 되고, 이 화음과 관계되는 C Major, C minor 그리고 A Major, A minor는 불균형한 울림이 생깁니다.
순정률(Just Intonation)
-각 음 사이의 비가 유리수 비율을 갖는 음률입니다. 이론적으로 1024 : 927의 비율로 조율된 음도 순정률이라고 할 수 있지만 실제로는 작은 정수들의 비로 조율된 음률만을 순정률이라고 합니다. 이렇게 작은 정수들의 비를 갖는 두 음은 그렇지 않은 두 음보다 협화음으로 들립니다.
Ex) 작은 정수의 비를 이용해 음계 전체를 조율할 수 있습니다. 예를 들어 G Major(사장조)를 조율하려면 먼저 완전 5도(G:D)와 완전 4도(G:C)를 각각 2:3과 3:4의 비율로 조율합니다. 그리고 나머지 음정은 16:15, 10:9, 9:8의 세 비율을 조합하여 만들 수 있습니다.
| G | A | B | C | D | E | F# | G |
| 9:8 | 10:9 | 16:15 | 9:8 | 10:9 | 9:8 | 16:15 | 9:8 |
*문제점
- 순정률은 울프 음정을 만들어내는 문제가 있습니다. 위의 조율에서는 C:A가 32:27의 좋지 않은 비율을 갖게 되고, E, A는 40:27의 더 나쁜 비율을 가지게 됩니다. A를 10/9만큼 낮추면 이 문제는 해결되지만 대신 D:A가 27:20이 되고 A:F#은 32:27이 됩니다. 이런 식으로 하나의 불협화음을 해결하면 다른 불협화음이 생기며, 이런 문제를 완전히 해결할 수 있는 방법은 사실상 없습니다.
평균율(Equal temperament)
-평균율은 옥타브를 똑같은 비율로 나눈 음률입니다. 제일 많이 쓰이는 것은 1옥타브를 12개의 평균한 음정으로 분할하고, 이를 반음으로 정하여 음계를 구성하는 12 평균율로, 대부분의 서양 조성 음악에 쓰입니다. 따라서 2개의 반음은 온음이 되고, 증 1도와 단 2도, 단 3도와 증 2도 등은 같은 간격으로 취급되므로 다른 이름한 소리의 취급이 필요하게 됩니다. 그러나 평균율은 순수하게 음 향악적으로 얻는 음과는 다르며, 그 예로 C#음이 Db음보다는 극소의 차이이나, 약간 높다는 것을 알 수 있습니다. 이러한 결점에도 불구하고 12 평균율은 일정한 악기로 어떠한 조로도 바꿀 수 있는 이점 때문에 전 세계적으로 보급된 것입니다. 이런 평균율의 발명은 다성 조음악, 무성 조 음악 등의 발전에 크게 공헌했고, 이후 음렬 주의 음악과 재즈의 발전에도 영향을 미쳤습니다.

그러나 평균율에서는 완전 8도를 제외한 어떤 음정도 협화음이 되지 않기 대문에 순정률만큼 사람의 귀에 아름답게 들리지 않습니다. 그 때문에 음을 기계적으로 조율할 필요가 없는 합창단이나 현악앙상블은 순정률에 가까운 조율을 사용합니다.
참고문헌 大学音乐理论 白秉東著, 위키피디아
'MUSIC STORY' 카테고리의 다른 글
| [Theory of Music] 음악의 정의- 음악의 형태 (0) | 2020.06.09 |
|---|---|
| [Theory of Music]음악의 정의- 음악의 요소 (0) | 2020.06.08 |
| [Theory of Music] Definition of Music 음악이론 악전 음악의 정의 (0) | 2020.05.31 |


